Overview

在机器学习(数据挖掘)领域，有两种算法，经常让初学者混淆，那就是：KNN分类和K-means聚类。而实际上这两种算法没有任何关系，只是名字里面都有一个K。下面，我们记录一下这两种算法，并分析一下它们的区别。

1.KNN分类

实际上KNN算法也可以用来做回归，但是我们这里只讨论分类。KNN全名是k-Nearest Neighbors，用法如下：
(1).将已经分好类的样本的特征输入，这些样本就是“参考样本”，也就是下一步的输入的未知样本的“邻居”；
(2).输入待分类样本，对于每个新样本，我们通过这个样本的周围最近的K个已经分好类的邻居的类别来判断它的类别。如果在这K个邻居中，某个类的数量最多，那么我们判断该样本为此类。
原则上二分类时，这个参数K取奇数为佳。一般情况下这个K取值不宜太小，以消除噪声影响，但是过大又会使分类边界模糊，所以这个K需要进行参数优化。原理图来自维基百科：

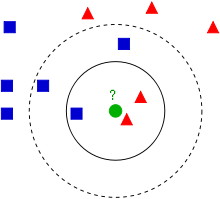
(3).这个被分好类的新样本，不作为下一个需要分类的样本的参照样本。且分类只次一次，不需要像K-means聚类那样迭代多次。
(4).一般情况下，我们在计算距离时，使用欧氏距离即可。

2.K-means聚类

K-means聚类是无监督的聚类算法。我们不知道这些样本的具体分类，也不知道具体有多少类。所以只能根据经验告诉程序或者软件，我们假设有K个分类。用法如下：

(1).我们假设样本有3类，即K=3.我们选择3个距离适当的坐标点作为这个3类的中心点(不一定必须是真实的点)。事实上，第一次选择的坐标点，将会很大程度上影响运算速度。如下图，我们选择红绿蓝3个坐标点为初始类中心点。

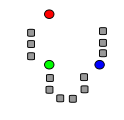
(2).将所有的待分样本按照最近邻原则分类。这是第一次迭代。

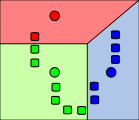
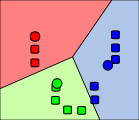
(3).这样，第一次分类结束。我们再根据最新的分类，计算出每个类中样本的平均坐标值，取为该类的新中心点。

(4).按照该方法，进行多次迭代，直到三个类的中心点收敛。这样，我们就得到这些样本的具体分类了。

3.两者之间的差异

两种算法之间有多种差异，如下：

• KNN为分类，K-means为聚类；
• KNN为监督学习，K-means为无监督学习；
• KNN的输入样本为带label的，K-means的输入样本不带label；
• KNN没有训练过程，K-means有训练过程；
• K的含义不同

两种算法之间有一点相似：
都是计算最近邻，一般都用欧氏距离。

这篇文章主要参考了以下几篇文章：
K-nearest neighbors algorithm
k-means clustering
Kmeans、Kmeans++和KNN算法比较

文章中所有图片均来自维基百科。